How Do You Tell What Gear Ratio You Have UPDATED

How Do You Tell What Gear Ratio You Have

Gear ratios and compound gear ratios

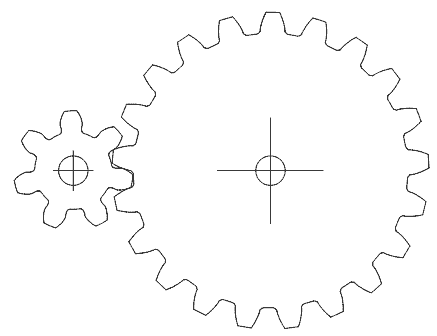
Working out simple gear ratios (2 gears)

A characteristic frequently requested in my gear program is that it should summate and display the gear ratio.

The reason it does non accept this feature is that the gear ratio is also the tooth count ratio (of the two gears), and that is a value that the user has to enter.

At left, the two meshing gears with 7 teeth and 21 teeth volition have a ratio of vii:21 (which is the same every bit 1:iii). That is to say, the seven-tooth gear volition plough iii times for ever ane turn of the 21-molar gear. The logic is simple, each gear needs to rotate past the aforementioned number of teeth for them to mesh, so the vii-molar gear, having one third the teeth, needs to turn three times as much

Determining what gears yous need
Suppose you have a motor that turns 1200 RPM (revolutions per minute), and yous need to turn something at 500 RPM.
The ratio y'all need is 500:1200, or five:12. All the same, simple gears with only five teeth tend to run a flake rough, so your best bet is to make (or obtain) gears with 10 and 24 teeth.

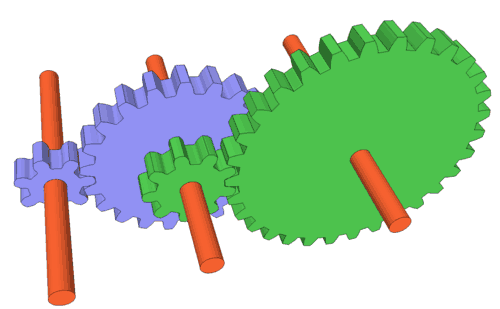
Determining compound gear ratios (multiple stages)

When a gear train has multiple stages, the gear ratio for the overall gearing system is the product of the individual stages.

For example, for the gear at left the blue gears are vii and 21 teeth, while the green gears are nine and thirty teeth. Thus, the showtime gear ratio is seven:21 and the second is nine:thirty. Multiplying the ii together gives (7x9):(21x30) = 63 : 630, which is one:x. And so the big light-green gear will brand ane turn for every 10 turns of the small blue gear.

Working out what gears you need for designing multiple stage gearing
Whatsoever gear ratio that can be achieved by multiple stages of gearing can too be produced by single stage gearing, but for large gear ratios, the large gear can go unwieldy.

There are many means to achieve a given reduction with multiple stages, but how to decide what tooth counts to use for the gears?

Suppose nosotros need a gear ratio that is i:11, and nosotros desire the smallest gear to accept no fewer than ten teeth. We could do this with a x-tooth and a 110-molar gear. Lets write the ratio as

x:110

Now, let's imagine we put another gear in between those. Let'southward imagine putting a 35 tooth gear between the 10 and the 110 tooth gears. The gear ratio between the 10 and the 110 tooth gears volition even so be the same, though the 10 and 110 tooth gears will now rotate in the same management, whereas before they turned in opposite directions.

With the 35-tooth gear in betwixt, we can now think of now having a x:35 tooth reduction, followed by a 35:110 tooth reduction.

Nosotros can reduce the 35:110 to vii:22, just if we don't want any gears smaller than x teeth, we need to double that to xiv:44. So we can at present brand our i:11 gearing with the following stages:

10:35   and  14:44

Total number of teeth between the two stages is 103 teeth, vs 120 for the original version. but more importantly, this gear prepare is smaller.

Common denominators are very important, and it may be necessary to pick a dissimilar intermediate tooth count to make reduction possible.. If, however, we wanted an xi : 127 gear ratio, the but way to get that exact ratio would exist with an eleven tooth and a 127 tooth gear (or multiples thereof), because both are prime number numbers that can't be factored.

On further consideration of the above ane:eleven gearing example, nosotros could have washed even ameliorate if nosotros instead started with 1:11 every bit 12:132. Nosotros could and then write this as 12:44 and 44:132, and the 44:132 is a ane:three ratio, which we could as well make a 10:xxx. That would leave us with 12:44 and 10:thirty, which adds up to just 96 teeth total. We could besides swap the two big gears if we wanted to. For example, x:44 and 12:30 multiplied together likewise produce a one:eleven ratio.

Design example 2: Gears for clock face 60 minutes and minute easily

Suppose nosotros want to make a one:12 reduction for a clock. 12 factors into 4 and 3, so we could do a 1:4 and a 1:iii reduction. but let'southward see if we can make the two ratios closer to each other.

Let's multiply both sides by 8, and then our 1:12 ratio becomes 8:96.
To get the reduction ratio for both gears, we want each gear ratio to be near the foursquare root of 12, which is about 3.464. Now 8 * 3.464 is 27.7. And then lets try 28 teeth for the intermediate gear.

So nosotros can write 8:28:96 or 8:28 and 28:96 We tin split up the right side by 4, so we get 8:28 and 7:24

It doesn't ever work out so nicely. Sometimes one side or the other doesn't have any common divisors, so you may demand to try different values for the intermediate.

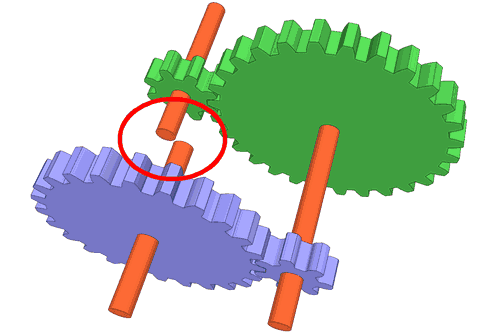For a clock, the hours and minute hands accept to exist concentric, so both of these gear pairs have to have the aforementioned shaft spacing. If we utilise the aforementioned molar pitch for both gears, the shafts will not line upwardly.

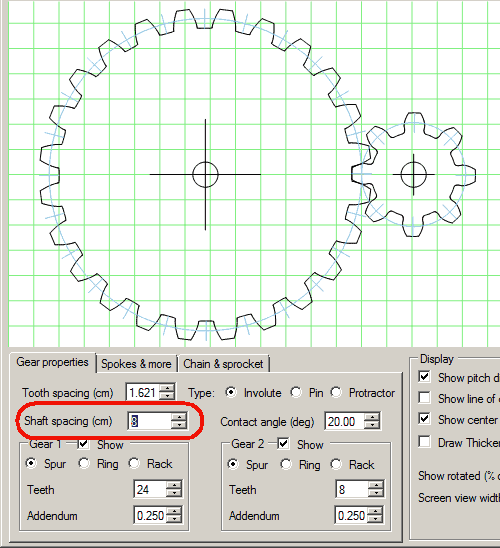Using my gear generator program, I tin can but enter the shaft spacing, and the programme will recalculate the tooth size accordingly. I used viii cm for both sets.

I cut the gears out of some x mm thick plywood on the bandsaw.

If I place them on elevation of each other, the two sets of gears expect about identical, only they have slightly different ratios, and the teeth on one set up are slightly larger.

A shaft through the larger gear on the right couples to the smaller vii-tooth gear behind it, and the shorter "hours" hand is screwed directly to the large gear.

Now, if I had a timer motor that turned i turn per hour, I could make a really big clock with these gears.

"Build a clock" is suggestion I often become. Maybe ane of these days I will build one, perchance non. No need to suggest it at any charge per unit, because the thought has certainly occurred to me :)

DOWNLOAD HERE

How Do You Tell What Gear Ratio You Have UPDATED

Posted by: johndognis.blogspot.com